Lec 7. Divide and Conquer

约 1058 个字 2 张图片 预计阅读时间 4 分钟

Divide and Conquer

1. Divide;
2. Conquer;
3. Combine.

分治法递归的时间复杂度递推公式通常具有如下形式：

\[ T(n) = a T(\frac{n}{b}) + f(n). \]

Substitution

推荐阅读

• Lec 7: Divide and Conquer - NoughtQ 的笔记本

即猜证。

Must prove the exact form.

做题时有换元的技巧。

Recursion Tree

设

\[ T(n) = a T(\frac{n}{b}) + f(n), \]

则

\[ T(n) = \Theta(n^{\log_b a}) + \sum_{i=0}^{\log_b n - 1} a^i f(\frac{n}{b^i}). \]

使用递归树进行证明；截自《算法导论》。

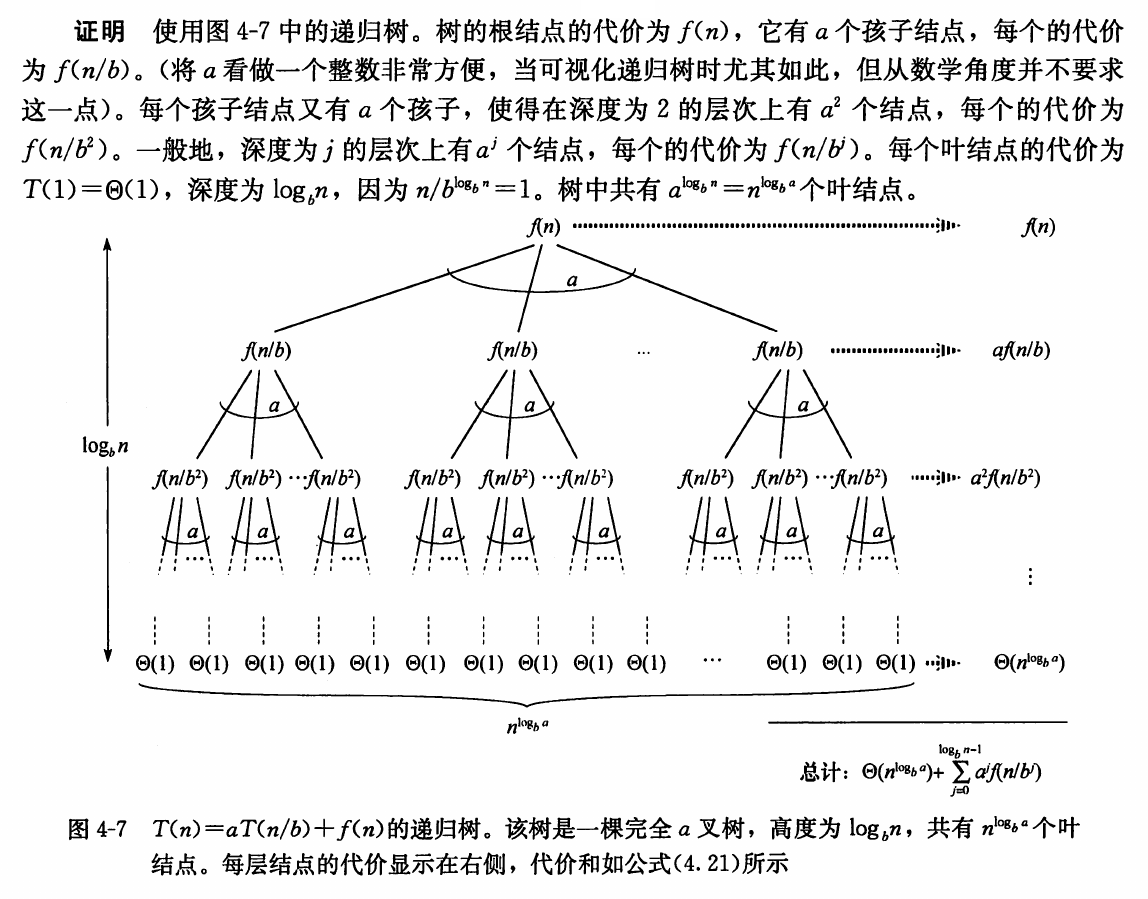
The Master Theorem

在此基础上使用一些数学（详见《算法导论》对应章节），可得主定理：

对于

\[ T(n) = aT(\frac{n}{b}) + f(n), a \ge 1, b \ge 2, \]

1. 若存在某个 \(\epsilon > 0\)，使得 \(f(n) = O(n^{\log_b a - \epsilon})\)，则 \(T(n) = \Theta(n^{\log_b a})\)；

2. 若 \(f(n) = \Theta(n^{\log_b a})\)，则 \(T(n) = \Theta(n^{\log_b a} \log n)\)；

3. 若存在某个 \(\epsilon > 0\)，使得 \(f(n) = \Omega(n^{\log_b a + \epsilon})\)，且对某个常数 \(c < 1\) 和所有足够大的 \(n\) 有 \(a f(n/b) \leq c f(n)\)，则 \(T(n) = \Theta(f(n))\)。

Tip

以下是一个更强的版本。

对于递推式

\[ T(n) = aT(\frac{n}{b}) + \Theta(n^k \log^p n), \]

其中 \(a \ge 1, b > 1, k \ge 0\)，\(p\) 为任意实数，

1. 若 \(a > b^k\)，则 \(T(n) = \Theta(n^{\log_b a}).\)
2. 若 \(a = b^k\)：
   • (a) 若 \(p > -1\)，则 \(T(n) = \Theta(n^k \log^{p+1} n);\)
   • (b) 若 \(p = -1\)，则 \(T(n) = \Theta(n^k \log \log n);\)
   • (c) 若 \(p < -1\)，则 \(T(n) = \Theta(n^k).\)
3. 若 \(a < b^k\)：
   • (a) 若 \(p \ge 0\)，则 \(T(n) = \Theta(n^k \log^p n);\)
   • (b) 若 \(p < 0\)，则 \(T(n) = \Theta(n^k).\)

The Closest Points Problem

Lemma: In the ClosestSplitPair subroutine, suppose \((p, q)\) is a split pair with \(d(p, q) < \delta\), where is the smallest distance between a left pair or right pair of points. Then:

• (a) \(p\) and \(q\) will be included in the set \(S_y\);
• (b) at most six points of \(S_y\) have a \(y\)-coordinate in between those of \(p\) and \(q\).

以上的 (b) 成立的原因；截自 Algorithm Illuminated。

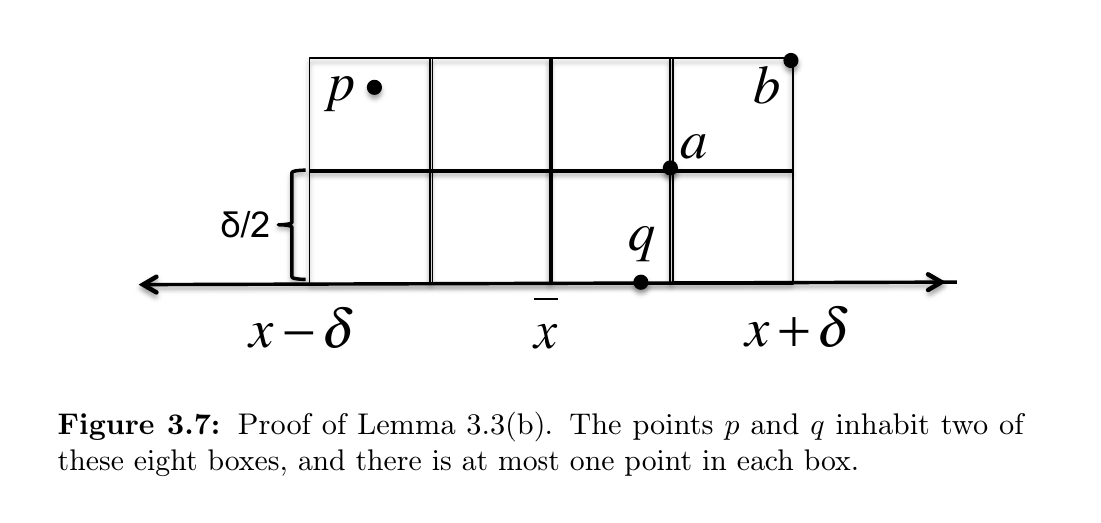
这是因为假设有两个点 \(a, b\) 同时处于一个格子中，则 \(d(a, b) \leq \frac{\delta}{\sqrt{2}} < \delta\)，与 \(\delta\) 的定义矛盾。

Tip

7 并不是最小的常数。实际上：

• 当前研究的点所在的一侧的所有点都完全可以不考虑，例如当前我们循环到了一个在左半边的点，那么整个左半边的点都不需要考虑，只需要考虑右半边 4 个格子最多的 4 个点。

• 还可以进一步将 4 这个数字降为 3。因为每在右半边放一个点，那么在右半边，以这个点为圆心半径为 \(\delta\) 的圆内不可能再有另一个点；最差的情况就是有四个这样的圆心，此时四个圆心在右半边区域的四个角上，这时找三个足够（其实就是 \((0, 0)\) 最好）；而其它情况不可能有四个圆心，最多三个圆心，找三个也足够。

K-way Merge Sort

在 2-way Merge 操作中我们使用了双指针法；同理，在 K-way Merge 操作中我们可使用 \(k\) 指针法，每次从 \(k\) 个指针中取出最小值。

朴素实现下每次取出最小值的操作是 \(O(k)\)。我们可以考虑维护一个堆（或锦标赛树），则每次取出最小值的时间复杂度为 \(O(\log{k})\)。设 \(k\) 个数组共有 \(n\) 个元素，则 K-way Merge 操作的总时间复杂度为 \(O(n \log{k})\)。

若 \(k\) 为常数，设整个 K-way Merge Sort 过程的时间为 \(T(n)\)，则

\[ \begin{align*} T(n) &= k T(\frac{n}{k}) + O(n \log{k}) \\ &= k T(\frac{n}{k}) + O(n), \\ \end{align*} \]

由主定理，\(T(n) = O(n \log{n})\)。

若我们关心 \(k\) 的影响，设整个 K-way Merge Sort 过程的时间为 \(T(n, k)\)，则

\[ T(n, k) = k T(\frac{n}{k}, k) + O(n \log{k}). \]

此时主定理不适用，我们需要画递归树进行求解。

递归树的高度 \(h = \log_{k}{n}\)，第 \(i\) 层（根节点为第 0 层）有 \(k^i\) 个子问题，每个子问题的工作量为 \(O(\frac{n}{k^i} \log{k})\)。

故总时间

\[ \begin{align*} T(n, k) &= \sum_{i = 0}^{h} k^i \cdot O(\frac{n}{k^i} \log{k}) \\ &= \sum_{i = 0}^{h} O(n \log{k}) \\ &= \log_{k}{n} \cdot O(n \log{k}) \\ &= \frac{\log{n}}{\log{k}} \cdot O(n \log{k}) \\ &= O(n \log{n}). \end{align*} \]

相较于二路，使用 \(k\) 路的好处在于递归树变矮，坏处在于每一层的合并工作变重。这里我们看到二者恰好抵消，最终总时间 \(T(n, k) = O(n \log{n})\)，与 \(k\) 无关。

Tip

在 In-Memory Sort 中，K-way Merge Sort 的常数很大，因为其需要维护一个最小堆。

K-way Merge Sort 通常用于 External Sort：当数据在硬盘上时，算法的瓶颈在于硬盘 I/O（相比之下在内存中维护一个最小堆的成本可忽略不计），而树高 \(h\) 决定了算法需要完整读写数据多少遍；此时我们希望减小树高 \(h\)，为此我们应使用大 \(k\)。

评论区